NuSCAP

Journées annuelles 2025

25 au 27 juin 2025, LS2N, Nantes

Orateurs : Xavier Allamigeon (Tropical, Inria Saclay, CMAP, École Polytechnique), Alexandre Goldsztejn (CNRS-LS2N, Nantes), Stef Graillat (LIP6, Sorbonne Université), Olivier Hénot (CMAP, École Polytechnique), Tom Hubrecht (Pascaline, LIP, ENS Lyon), Mioara Joldes (CNRS-LAAS, Toulouse), Guillaume Melquiond (Toccata, Inria Saclay), Arnaud Minondo (MAX, LIX, École Polytechnique), Josué Moreau (Toccata, Inria Saclay), Bruno Salvy (Pascaline, Inria Lyon, LIP, ENS Lyon).

Comment venir

La rencontre se déroulera sur le campus Sciences de Nantes Université, dans l'amphithéâtre situé au rez-de-chaussée du bâtiment 34.

En tram: Le campus est en particulier desservi par le tram 2, arrêt Michelet Sciences. Pour arriver au bâtiment 34 depuis cet arrêt, marcher tout droit et dépasser le restaurant universitaire puis le laboratoire Jean Rouxel sur votre droite, et enfin la BU sur votre gauche, pour prendre à droite la rue qui descend franchement du grand terre-plein central arboré. Le bâtiment 34 sera sur votre droite, relié par une passerelle à son voisin plus ancien le bâtiment 11.

À pied: On peut aussi arriver directement au bâtiment 34 depuis les (jolis) bords de l'Erdre. En venant du centre-ville, il faut tourner à gauche au niveau du bâtiment du club Nantes Université Aviron, pour le contourner. Longer brièvement le parking avant de rentrer dans le campus qui se trouver sur la gauche, en prenant le chemin piéton qui monte franchement sur quelque mètres. Le bâtiment 34 se trouve sur votre gauche.

Déjeuners

Sur la carte ci-dessous, le point vert est le bât. 34, lieu des exposés, et le point rouge est le restaurant universitaire La Lombarderie, où nous déjeunons. N'oubliez pas votre contremarque, il n'est pas possible de payer par carte!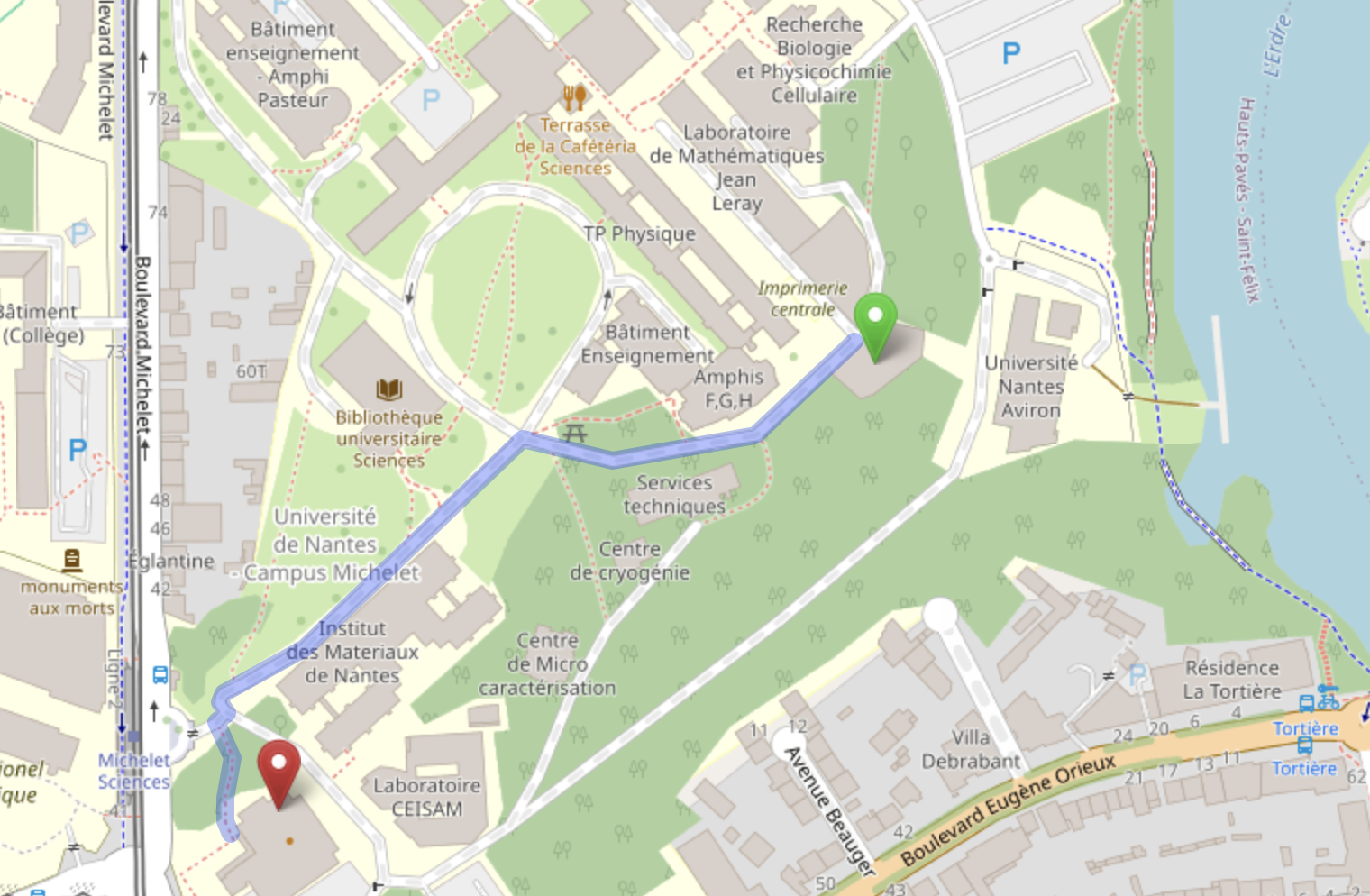

Programme

Mercredi 25 juin

• 09:00. Accueil café
• 10:00. Mioara Joldes (CNRS-LAAS, Toulouse), Optimization-Aided Construction of Multivariate Chebyshev Polynomials
  résumé

  This talk is concerned with an extension of univariate Chebyshev polynomials of the first kind to the multivariate setting, where one looks for best approximants to specific monomials by polynomials of lower degree relative to the uniform norm. Exploiting the Moment-SOS hierarchy, we devise a semidefinite-programming-based procedure to compute such best approximants, as well as associated signatures. Applying this procedure in three variables leads to the values of best approximation errors for all monomials up to degree six on the euclidean ball, the simplex, and the cross-polytope. Inspired by numerical experiments, we obtain explicit expressions for Chebyshev polynomials in two cases unresolved before. This is joint work with M. Dressler, S. Foucart, E. de Klerk, J.-B. Lasserre and Y. Xu.

• 11:00. Guillaume Melquiond (Toccata, Inria Saclay), Floating-point error analysis using CoqInterval
  résumé

  CoqInterval is a set of strategies for the Rocq proof assistant to help reasoning about inequalities of real-valued expressions. It was originally designed to automatically prove error bounds on method errors. To do so, it can compute reliable polynomial approximations using Taylor models, among other things. But lately, it has gained the ability to reason about rounding errors too. During this talk, I will show how the library can be used to formally verify the correctness of fixed- and floating-point code, and how it differs from related tools like Gappa.

• 12:00. Déjeuner au restaurant universitaire Lombarderie
• 14:00. Josué Moreau (Toccata, Inria Saclay), A safe low-level language for computer algebra and its formally verified compiler
  résumé

  I will present Capla, a programming language for writing low-level libraries for computer algebra systems. Such libraries (GMP, BLAS/LAPACK, etc) are usually written in C, Fortran, and Assembly, and make heavy use of arrays and pointers. The proposed language is halfway between C and Rust with a type system similar to the one of SPARK. It does not have any undefined behavior and is designed to ease the deductive verification of programs, while being low-level enough to be suitable for this kind of computationally intensive applications. I have also implemented a compiler for this language, based on the CompCert compiler. The safety of the language has been formally proved using the Rocq proof assistant, and so has the property of semantics preservation for the compiler.

• 15:00. Olivier Hénot (CMAP, École Polytechnique), A Computer-Assisted Proof Approach to Continuation
  résumé

  In this talk, we present computer-assisted proof (CAP) techniques to solve systems of parameterized nonlinear equations of the form F(x(λ), λ)=0. This setup covers a wide range of problems in dynamical systems -- be it equilibria, periodic orbits, or connecting orbits. Rubber hits the road when it comes to verifying the hypotheses of the implicit function theorem beyond a local neighborhood. An other strategy relies on rigorous numerical techniques. We will start by reviewing some fundamental CAP principles, particularly those based on the contraction mapping theorem. Next, we will see how a series expansion with respect to the parameter can give us entire branches of solutions in one go. The continuation of a family of solutions often runs into branch splitting (bifurcations). Desingularization techniques allow us to isolate and follow a specific branch, the method presented here can then be used to go directly through the bifurcation point. This contrasts with the standard approach of performing a local analysis near the bifurcation separately, and then "gluing" the solution branches back together.

• 16:00. Pause café
• 16:30. Atelier: Comment fait-on des preuves en 2025 ? Comment voudrait-on en faire dans le futur ?

Jeudi 26 juin

Matinée

• 09:30. Tom Hubrecht (Pascaline, LIP, ENS Lyon), Polynomial approximation with size-constrained coefficients
  résumé

  To design a libm (mathematical library), one needs to devise precise and fast evaluations of different mathematical functions. This is usually done in two steps, first operating a range reduction to reduce the input space to a small interval and then using a tight polynomial approximation to complete the computation. Those polynomial approximations are however constrained, as each of their coefficients must fit in one (or several) floating-point values. This talk will introduce the tools necessary for designing such constrained approximations and explain how Euclidean Lattices and orthogonal projections in function spaces help us achieve this goal.

• 10:30. Pause café
• 11:00. Xavier Allamigeon (Tropical, Inria Saclay, CMAP, École Polytechnique), A formal disproof of the Hirsch conjecture
  résumé

  In this talk, I will present a formal verification of counterexamples of Santos et al. to the so-called Hirsch Conjecture on the diameter of polytopes (bounded convex polyhedra) in the proof assistant Rocq. In contrast with the pen-and-paper proof, our approach is entirely computational: we implement in Rocq and prove correct an algorithm that explicitly computes, within the proof assistant, vertex-edge graphs of polytopes as well as their diameter. Our approach relies on a careful balance between the simplicity of the algorithm (to make the formal proof easier) and its efficiency (to scale to polytopes with a large and intricate combinatorial structure).

  I will also discuss recent (but not yet formally proved) improvements to the algorithm, that reduce the performance gap with state-of-the-art (informal) methods to a factor ~10. In particular, I will explain how the performance of numerical computations in Rocq have challenged the standard optimization techniques used in polyhedral computations.

  Joint work with Quentin Canu and Pierre-Yves Strub.

• 12:00. Déjeuner au restaurant universitaire La Lombarderie

Après-midi

• 14:00. Bruno Salvy (Pascaline, Inria Lyon, LIP, ENS Lyon), Positivity Proofs for Linear Recurrences through Contracted Cones
  résumé

  Deciding the positivity of a sequence defined by a linear recurrence with polynomial coefficients and initial conditions is difficult in general. Even in the case of recurrences with constant coefficients, it is known to be decidable only for order up to 5. We consider a large class of linear recurrences of arbitrary order, with polynomial coefficients, for which an algorithm decides positivity for initial conditions outside of a hyperplane. The underlying algorithm constructs a cone, contracted by the recurrence operator, that allows a proof of positivity by induction. The existence and construction of such cones relies on the extension of the classical Perron-Frobenius theory to matrices leaving a cone invariant.

  This is joint work with Alaa Ibrahim

• 15:00. Atelier : NuSCAP, suite mais pas fin.
• 16:00. Pause café
• 16:30.
• 20:00. Dîner au restaurant Baron Lefèvre

Vendredi 27 juin

Matinée

• 10:00. Stef Graillat (LIP6, Sorbonne Université), Condense and Distill: fast distillation of large floating-point sums via condensation
  résumé

  Floating-point summation is a fundamental task at the heart of many scientific computing applications. When the sum is very ill conditioned, computing it accurately can become challenging. One can employ distillation methods, which consist in transforming an ill-conditioned sum into an equivalent but well-conditioned one. However, distillation is a very expensive process. In this talk, we propose Condense and Distill, a new distillation method that relies on a preprocessing step that we call condensation, because it transforms the original sum into a far smaller sum, which can then be distilled inexpensively. This condensation step exploits a new, key observation that floating-point addition is exact when the addends have both the same exponent and the same least significant bit. Condense and Distill thus requires accessing the exponent field of the summands. Compared with state-of-the-art summation methods with the same requirement such as the Demmel--Hida method [J. Demmel and Y. Hida, SIAM J. Sci. Comput., 25 (2003), pp. 1214--1248], Condense and Distill presents the significant benefit of running entirely in the working precision, with no need for extra precision. At the same time, it preserves the main advantages of the Demmel--Hida method compared with other methods, in particular those based on error-free transformations such as AccSum [S. M. Rump, T. Ogita, and S. Oishi, SIAM J. Sci. Comput., 31 (2008), pp. 189--224]: namely, its cost is independent of the conditioning, and it exhibits near perfect parallel scaling. We present numerical experiments that confirm that Condense and Distill can reliably and efficiently distill large ill-conditioned sums and performs favorably compared with other state-of-the-art summation methods.

  This is a joint work with Théo Mary.

• 10:30. Pause café
• 11:00. Arnaud Minondo (MAX, LIX, École Polytechnique), Matryoshka arithmetic
  résumé

  Interval arithmetic achieves numerical reliability for a wide range of applications, at the price of a performance penalty. For applications from differential equations to homotopy continuation, one key ingredient is the efficient and reliable evaluation of complex polynomials represented by straight-line programs (SLPs). This is best achieved using ball arithmetic, a variant of interval arithmetic. In this talk, we introduce new variants of ball arithmetic. For the evaluation of SLPs, this allows us to almost eliminate the overhead of ball arithmetic with respect to direct numerical evaluations.

• 12:00. Déjeuner